25 ++ 等比数列 一般項 まとめ方 115828-等比数列 一般項 まとめ方

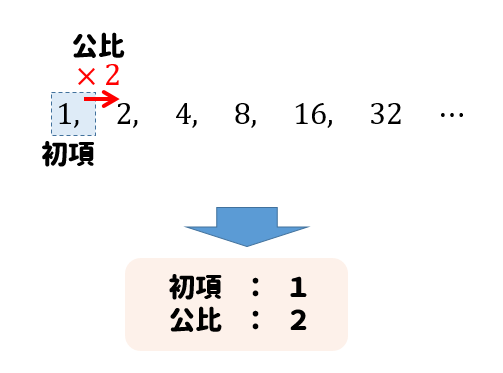
そして一般項は $a_n=a_1(n1)d$ となります。 22等比数列 等比数列 とは、となり合う数字どうしを割ると、その商（割り算の答え）が同じになるような数字の並び方のことです。等比数列とは？一般項や和の公式、シグマの計算問題などを 数列の和SnとAnの式から一般項を求める方法 等比数列まとめ和の公式の証明や一般項の求め方を解説 数列の和から一般項の解法 夢を叶える塾;等比数列の一般項を求める 等比数列の一般項を求める例を見てみましょう。 ここに等比数列があります。 3 , 6 , 12 , 24 , 48 この数列は「初項3、公比2の等比数列」です。 ここで等比数列の一般項の公式を思い出してみましょう。

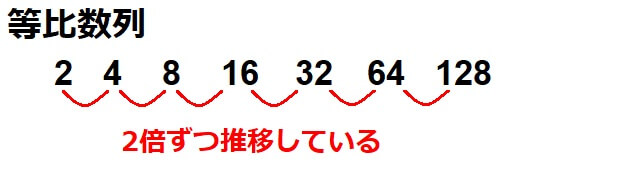
等比数列

等比数列 一般項 まとめ方

等比数列 一般項 まとめ方-一般項の求め方 等差数列、等比数列の一般項の求め方を下記に示します。 aは初項、nは第n項、dは公差、rは公比といいます。公差d、公比rの求め方は下記が参考になります。 公差とは？1分でわかる意味、一般項、n項、等差数列との関係 公比とは？等比数列の一般項{an}は初項aに公比rを(n1)回かけたものだから $an = ar^{n1}$ r = 1の時は、$ar^0$となり $a × 1$となるため初項が求まります。

漸化式全パターンの解き方まとめ 難しい問題を攻略しよう 受験辞典

初項 a, 公比 r の等比数列の一般項 an は an=a･rn1 注意　上式で，r≠0，n=1 のときは，r0=1 と決めます。 例題１　等比数列 {an}において，初項 3，a4=375 の公比 r と一般項 an を求めよ。② 等比数列型の漸化式の解き方 等比数列型の漸化式を用いる前にまずは等比数列の一般項の公式を思い出しておきましょう。 等比数列の一般項は で求めることができました。 漸化式では初項と公比を求めることができ、それを用いて基本の等比数列の等比数列の公式まとめ（一般項・和の公式・証明） 等比数列の和の公式の覚え方とは？問題を通してわかりやすく証明 やさしい無限等比級数の応用問題 ～16年度豊橋科学技術

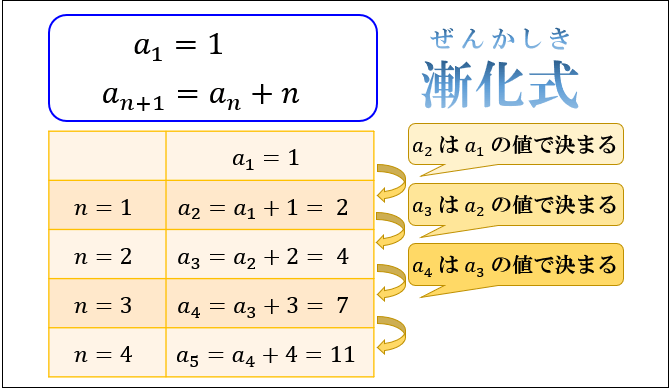
高校数学B 数列：漸化式17パターンの解法とその応用 漸化式 ( ぜんかしき )は、数列分野の最重要事項である。 大学受験という観点からすると、高校数学全体から見ても最重要事項の1つといえる。 要するに大学受験における出題頻度が極めて高い。 そのIf playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to漸化式初級編・基本4形態 " 等比数列型 S 等比数列型 an1 = pan 解法と解説 この漸化式は，第n 項をp 倍すると第n 1 項になることを意味するので，公比p の等比数列を表している．し たがって，一般項an は， an = a1p n¡1 である． g q I2 次の漸化式で定義される数列fang の一般項を求め

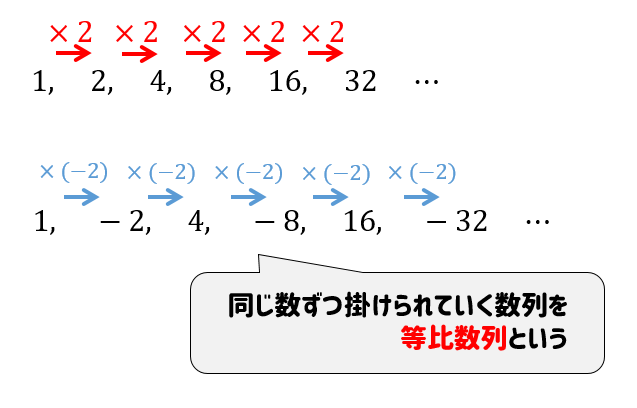
5 数列 数が一列に並んだものを数列といいます1 ．高校で，漸化式が与えられたときに一般項を求める方法を いくつか習いました．例えば，初項a，交差d の等差数列の第n 項（一般項）は，an = a(n−1)d とな りますし，初項a，公比r の数列の一般項はan = arn¡1 です．今回の講義では，数列を（1等比数列の導入と一般項 数列の中で，比が等しい数列のことを等比数列といいます．その比を 公比 といい，英語でratioというので，よく r r と表します．以下の図のようになります． n n 番目である an a n がこの数列の 一般項 になります． an a n を求める 差が一定の数列が等差数列ならば，比が一定の数列が等比数列です。 等比数列の一般項 隣り合う項の比\(\displaystyle \frac{a_{n1}}{a_{n}}\)が常に一定である数列を等比数列といい，\(\displaystyle \frac{a_{n1}}{a_{n}}=r\)を公比という

等比数列の和の公式の証明といろいろな例 高校数学の美しい物語

等差 等比 の和 2次式 等比 の和 おいしい数学

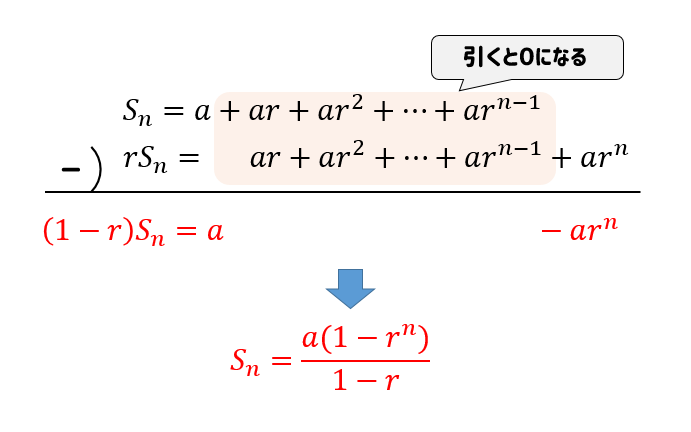
 等比数列の一般項を求める公式 $$a_n=ar^{n1}$$ $$a初項 r公比$$ 等比中項 3つの項の等比数列\(a, b, c\)について、次の式が成り立つ。 $$b^2=ac$$ 等比数列の和を求める公式 \(r\neq 1\) のとき $$S_n=\frac{a(1r^n)}{1r}=\frac{a(r^n1)}{r1}$$ \(r=1\) のとき $$S_n=na$$等比数列の一般項 この等比数列の第 n 項つまり一般項 an は 「初項から第 n 項までには r を n − 1 個かける」 と考えて an = arn − 1 となるのはすぐにわかるだろう． また，漸化式 (1) から一般項 an を求める方法もみておこう． STEP1 漸化式 (1) の n に 1, 2 a 1 = 7 × 27, a 2 = 5 × 9, a 3 = 3 × 3, a 4 = 1 × 1, 一般的には，等差数列 { b n } と等比数列 { c n } があって，一般項が a n = b n c n となっている数列 { a n } のことを「 等差×等比型の数列」と呼んでいます． なお，本来このような数列に名前がついていませんが，この記事では「 等差×等比型の数列」という表現を用います．

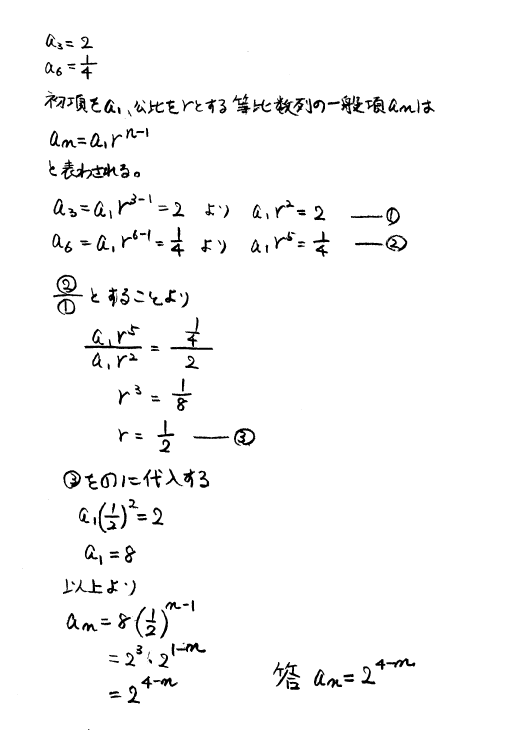
等比数列 一般項

An 1 Pan Q型の数列の一般項の求め方 等比数列型に帰着させる

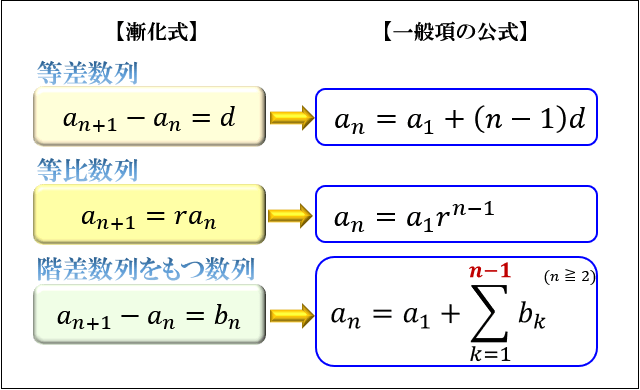
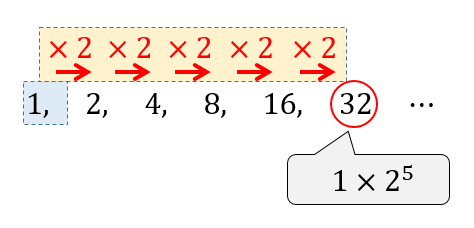
⇒ 等差数列 一般項と和の公式の求め方と最大値へのグラフ利用 等差数列の和が何次関数になるのか確認しておいてください。 等比数列の一般項と和 1つの数に次々と同じ数をかけるという手順で得られる数列を等比数列といいます。 ここまで、等比数列の一般項の求め方と和の公式を説明したあとに、大学受験でよく出題される問題を説明してきました。 等比数列は基本をきちんと理解できれば、あとはひたすら問題を解いて考え方になれることが重要になってきます。 この記事で理解したことをもとに、問題集や行きたい大学の過去問などで練習してみてください！ みなさんが等比1．等差数列 一定の差で増える（もしくは減る） 一般項：a n =a＋(n̠̠－1)d （例）1,3,5,7,9, ‥‥ 2．等比数列 一定の比で増える（もしくは減る） 一般項：a n =ar n1 （例）2,4,8,16,32, ‥‥ 3．階差数列

かけずらをするまでは分かったのですが Clear

無限等比級数とは 基本からわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

等比数列の一般項は？ 等比数列（とうひすうれつ）の一般項は下式で計算します。 aは初項、rは公比（一定の数）、nは第n項のことです。 初項a、公比rが決まれば、より具体的な等比数列の一般項が算定できます。 さらに、nに値を代入すれば特定の項の値を算定できます。 例えば です。 2×5 (n－1) を10 (n－1) にしないよう注意してくださいね。 2×5 (n－1) ≠10 (nの等比数列になるので，一般項 を特性方程式と呼び，その解 を求めるという覚え方があります． これは，一般によく使われる解き方ですが，「特性方程式」や「その解」が何を表しているのかということを消化不良のまま使ってしまうと，危険な 等比数列の和をあつかう問題を解くときは公式を覚えているだけでよいですが，後に登場する一般項が\((等差数列)\times (等比数列)\)の数列の和を求める場合も同じテクニックを使うので，できるようにしておいた方がよいです。 \(r\neq 1\)のときしか使えない

数列とは 数列の基本とポイントを解説

等比数列の項数の出し方でわからないところがあります 画像を見て頂きたい Yahoo 知恵袋

これは等差数列の和を求める公式と同じ考え方です。 1から100までを等差数列と考えると、初項が1、末項(一番最後の項)が100で、これを足すと101。そしてこれが100項の半分50項あるので、101×50 つまり一般の等差数列n項の和は、(初項＋末項)×1/2n となります。最後に，等比数列の和の公式を使ったいろいろな応用例を紹介します。 難しい数列の和の計算に応用する ・等差数列×等比数列の和は求まる。 ∑ k = 1 n k p r k \displaystyle\sum_{k=1}^nk^pr^k k = 1 ∑ n k p r k というタイプの和です。 {bn}の一般項は前回「等差・等比・階差数列型の一般項の求め方」と同じ方法等比数列型の漸化式を解くことで導出して、 \(b_{n}=12× 2^{n1}\) bn＝12×2^(n1)となります。 12＝2・2・3より \(b_{n}=3× 2^{n1}\) これでbnが計算出来たので、bnとAnの関係を思い出して、《bn＝an4》より、 \({an}の一般項はa_{n}=3× 2^{n1}4\)と求める事ができました。

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

等 比 数列 漸 化 式 Documents Openideo Com 数学b 高速トレーニング 漸化式 群数列編 東進ブックス 大学受験 高速マスター 大吉 巧馬 本 Documents Openideo Com

なんで初項2 公比2の等比数列とわかるのですか Clear

漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

等比数列の一般項について この回答の仕方では不正解なんですか 等 数学 教えて Goo

等差数列 等比数列の一般項とその和の求め方 Webstation Plus

等比数列の一般項は 1分でわかる求め方 和の計算 等差数列との違い

高校数学 B 数列 応用問題にも使える 等比数列の和を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学

等比数列の和から一般項の求め方 １ 高校数学ｂ Youtube

この等比数列の一般項の問題で カッコがつくときとつかないときどこで見分けるんですか Clear

数列と級数 Of 京極一樹の数学塾会員頁

階差型の数列 おいしい数学

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

詳説 数学ｂ 等差数列 等比数列 高校生 数学のノート Clear

等比数列

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

高校数学b 等比数列 A N の和 １ 映像授業のtry It トライイット

高校数学b 等差中項 等比中項の関係式 映像授業のtry It トライイット

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

等比数列の一般項と和 おいしい数学

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

等比数列

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

高校数学b 等比数列 A N の和 ２ 映像授業のtry It トライイット

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

高校数学ｂ 漸化式 基本パターン 等差 等比 階差 特性方程式 学校よりわかりやすいサイト

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

3

高校数学b 等比数列をなす3数の3通りの表現 等比中項 受験の月

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

高校数学b 適当に並び替えると等差数列にも等比数列にもなる3数 受験の月

漸化式全パターンの解き方まとめ 難しい問題を攻略しよう 受験辞典

等比数列の和 末項

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

Sシグマの公式まとめと計算方法 数列の和の公式 理系ラボ

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列の公式まとめ 一般項と和の公式を分かりやすく解説

等比数列の一般項の問題です 解説をよろしくお願いします Clear

漸化式全パターンの解き方まとめ 難しい問題を攻略しよう 受験辞典

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

高校数学b 等差数列と等比数列の共通項の数列の一般項 受験の月

等比数列の一般項の問題です 解説をよろしくお願いします Clear

メルカリ 高校数学b 数列 ベクトル まとめノート 参考書 2 500 中古や未使用のフリマ

等比数列の一般項と和 おいしい数学

高校数学b 数列 ベクトル まとめノートの通販 By Prince 医療系資格取得応援 ラクマ

1

漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

無限 等 比 級数 の 和 等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Documents Openideo Com

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

等比数列の和の公式の覚え方とは 問題を通してわかりやすく証明 極限についても考察 遊ぶ数学

数学の疑問を解決するブログ 和から一般項を求める数列

等差 等比数列の和 数学 B 数列 Youtube

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列

等比数列 一般項や和の計算 数学の偏差値を上げて合格を目指す

高校数学b 等比数列 A N の一般項 １ 映像授業のtry It トライイット

漸化式全パターンの解き方まとめ 難しい問題を攻略しよう 受験辞典

5講 等比数列の和 1節 等差数列と等比数列 問題集 3章 数列

中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

3

高校数学 B 数列 等比数列の基本性質と一般項 やはり俺の考察ブログはまちがっている アニメ 数学

等比数列の一般項と和 おいしい数学

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

高校 数学b 数列８ 等比数列の一般項１ １６分 Youtube

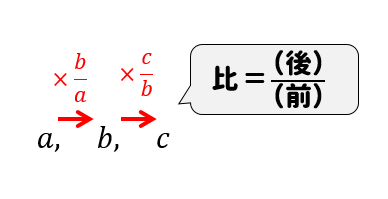
等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

高校数学ｂ 漸化式 基本パターン 等差 等比 階差 特性方程式 学校よりわかりやすいサイト

等比数列とその一般項 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開

Q Tbn And9gcrhoqs Tiaw74o0thwqpqqyulvy4xv5hy7apwesqqy4i H6wzaw Usqp Cau

高校数学b S と等差 等比数列の和 映像授業のtry It トライイット

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

2

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列の一般項の答えが写真の のようにに答えが出たときどちらのように表記する Yahoo 知恵袋

等比数列の一般項と和 おいしい数学

等比数列

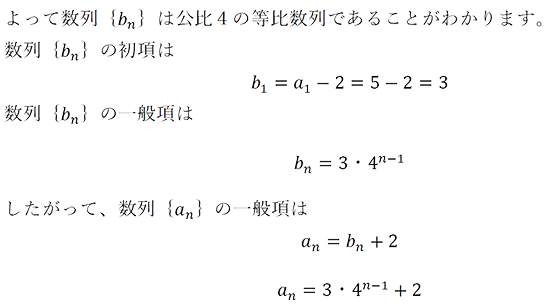
漸化式の解き方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等比数列の公式まとめ 一般項と和の公式を分かりやすく解説

漸化式全パターンの解き方まとめ 難しい問題を攻略しよう 受験辞典

高校数学b 等比数列の一般項 A N Ar N 1 受験の月

漸化式の意味と解き方 一般項の求め方を12パターンまとめて解説

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列の和について 数学 苦手解決q A 進研ゼミ高校講座

数列と級数 京極一樹の数学塾

Incoming Term: 等比数列 一般項 まとめ方,